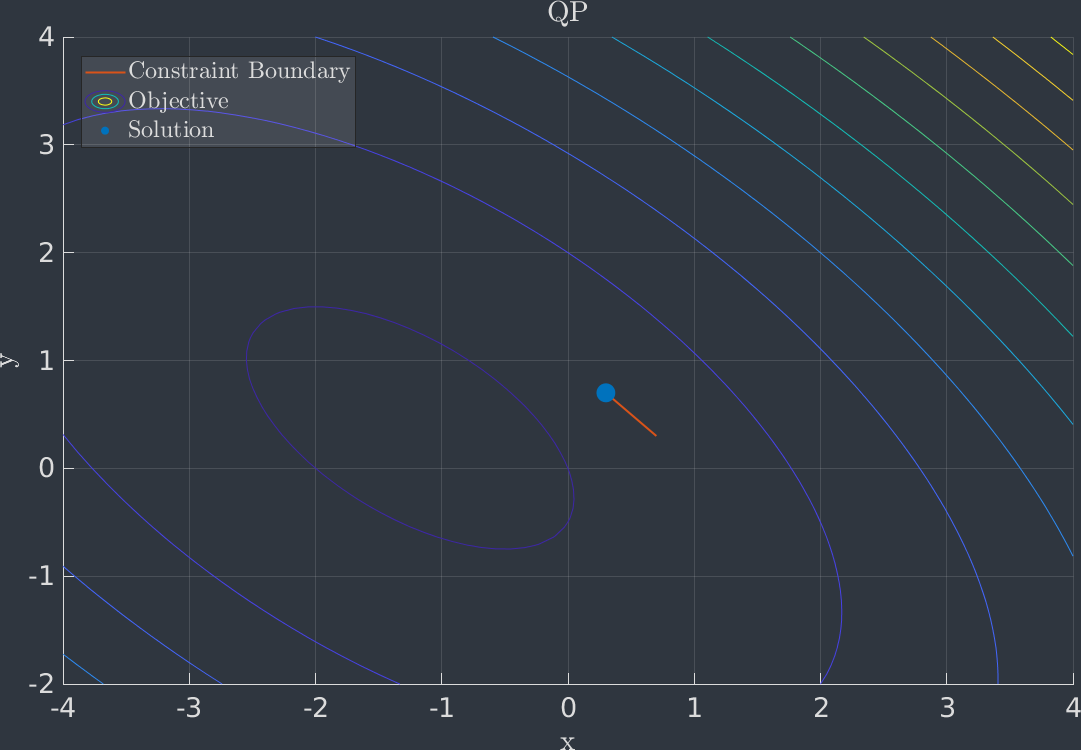
Quadratic Programming problem

scs-eigen can be used to solve Quadratic Programming (QP) problems in the for

\[ \begin{array}{rl} \text{minimize } & \frac{1}{2} x^\top P x + q^\top x + r \\ \text{subject to } & l \le A x \le u \end{array} \]

where $x \in \mathbb{R}^n$ is the optimization variable. The objective function is defined by a positive semidefinite matrix $P \in S^n_+$ and vector $q \in \mathbb{R}^n$ . The linear constraints are defined by matrix $A \in \mathbb{R}^{m \times n}$ and vectors $l$ and $u$ so that $l_i \in \mathbb{R} \cup \{-\infty\}$ and $u_i \in \mathbb{R} \cup \{\infty\}$ for all $i \in \{1,...,m\}$ .

The following example shows how scs-eigen can be used to solve the QP problem:

\[ \begin{array}{rl} \text{minimize } & \frac{1}{2} x^\top \begin{bmatrix} 3 & 2 \\ 2 & 4\end{bmatrix} x + \begin{bmatrix} 3 & 1 \end{bmatrix} x \\ \text{subject to } & \begin{bmatrix} 1 \\ 0 \\0 \end{bmatrix} \le \begin{bmatrix} 1 & 1\\ 1 & 0 \\0 & 1 \end{bmatrix} x \le \begin{bmatrix} 1 \\ 0.7 \\0.7 \end{bmatrix} \end{array} \]
Image

First of all you should include ScsEigen

#include <ScsEigen/ScsEigen.h>

You can also define the Hessian, gradient the constraint matrix and vectors.

Eigen::Matrix2d H;
H << 3, 2,
     2, 4;
Eigen::Vector2d gradient;
gradient << 3, 1;

Eigen::MatrixXd A(3,2);
A.setZero();
A(0,0) = 1;
A(0,1) = 1;
A(1,0) = 1;
A(2,1) = 1;

Eigen::Vector3d lowerBound;
lowerBound << 1, 0, 0;

Eigen::Vector3d upperBound;
upperBound << 1, 0.7, 0.7;

Once the matrices used to described the QP problem have been defined you can create ScsEigen::Solver and initialize the number of variables.

ScsEigen::Solver solver;
solver.setNumberOfVariabels(2);

Now you can set the constraints and the cost using ScsEigen::MathematicalProgram class

solver.mathematicalProgram().addLinearConstraint(
        std::make_shared<ScsEigen::LinearConstraint>(A, lowerBound, upperBound),
        "linear constraint");

solver.mathematicalProgram().addQuadraticCost(
        std::make_shared<ScsEigen::QuadraticCost>(H, gradient),
        "quadratic cost");

You can finally solve the problem and get the solution

solver.solve();
Eigen::Vector2d solution = solver.solution().solution;

The complete example follows

### CMakeLists.txt
project(QP)
find_package(ScsEigen REQUIRED)
add_executable(QP qp.cpp)
target_link_libraries(QP ScsEigen::ScsEigen)
/// qp.cpp

#include <ScsEigen/ScsEigen.h>

#include <Eigen/Dense>

int main()
{
    Eigen::Matrix2d H;
    H << 3, 2,
         2, 4;

    Eigen::Vector2d gradient;
    gradient << 3, 1;

   Eigen::MatrixXd A(3,2);
    A.setZero();
    A(0,0) = 1;
    A(0,1) = 1;
    A(1,0) = 1;
    A(2,1) = 1;

    Eigen::Vector3d lowerBound;
    lowerBound << 1, 0, 0;

    Eigen::Vector3d upperBound;
    upperBound << 1, 0.7, 0.7;

    ScsEigen::Solver solver;

    solver.mathematicalProgram().setNumberOVfariables(2);

    if (!solver.mathematicalProgram().addQuadraticCost(
        std::make_shared<ScsEigen::QuadraticCost>(H, gradient),
        "quadratic cost"))
        return EXIT_FAILURE;


    if (!solver.mathematicalProgram().addLinearConstraint(
        std::make_shared<ScsEigen::LinearConstraint>(A, lowerBound, upperBound),
        "linear constraint"))
        return EXIT_FAILURE;

    if (!solver.solve())
        return EXIT_FAILURE;
    if (!solver.solution().isValid())
        return EXIT_FAILURE;
    if (solver.solution().status != ScsEigen::Solution::Status::solved)
        return EXIT_FAILURE;

    Eigen::Vector2d solution = solver.solution().solution;

    return EXIT_SUCCESS;
}